Course description
Rectilinear flow of heat along a bar:
Let a long metal bar of uniform cross-section is heated steadily at one end M and the bar is so long that the other end N may be regarded to be at the same temperature as that of the surroundings (Fig. 8). Now we shall consider two neighboring planes at P and Q at distances x and from the hot end, therefore we have considered a layer PQ. Let θ be the excess temperature of the layer at P over the surroundings, and dθ/dx be the temperature gradient at that point. For convenience, we shall assume that θ and x are increasing together. Then the excess temperature of the plane at Q over the surroundings will be (θ+dθ/dx δx) and the temperature gradient at that point is d/dx(θ+dθ/dx .
Out of this amount of heat gained by the layer, a part is absorbed in raising the temperature of the layer and the rest is radiated out of the surface.
If ρ and s are the density and specific heat of the material of the bar respectively, and if dθ/dt is the rate of increase of temperature of the material of the bar, then the quantity of heat required per second to raise the temperature of the element
= mass × specific heat × rate of rise in temperature
= volume × density × specific heat × rate of rise in temperature
=A. δx. ρ.s.dθ/dt
According to Newton’s law of cooling, heat lost by radiation per second from the surface of the bar
= emissive power × surface area × average temperature excess over the surroundings
= E.p. δx. θ
where, E = emissive power or emissivity of the surface of the bar. (Defined as the quantity of heat radiated from the surface per second per unit area per unit temperature difference with the surroundings.)
p = the perimeter of the section of the bar, therefore,
p. δx = surface area of the section of the bar
and θ = average excess temperature of the section of the bar over that of the surroundings.
Eqn. (ii) is the standard (Fourier) equation for one dimensional flow of heat in the variable (periodic) state.
Steady state: (The state, when the metal bar will no longer utilize any heat for its warming; all the heat received from the source being lost to the surroundings by radiation. Thus heat flowing in will be equal to the heat flowing out, i.e., q1 = q2 and θ1 = θ2)
When the steady state is reached there is no change in temperature with time, i.e., dθ/dt=0. Therefore, Eqn. (ii) becomes
h (d^2 θ)/dx^2=μθ
(d^2 θ)/dx^2=μ/h θ -------------------------------(iii)
Eqn. (iii) represents the heat flow in the steady state when the heat loss due to radiation is not negligible.
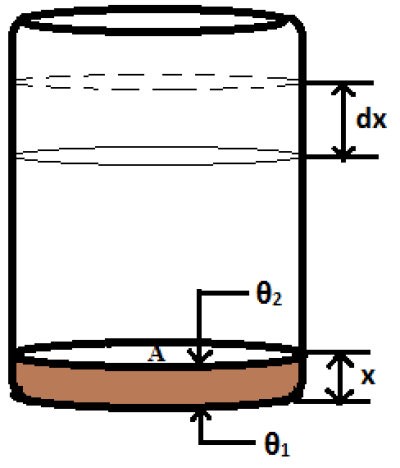
Problem 1: A rectangular steel tank has 2 mm thick bottom. Water in it is boiled and the level of water falls at the rate of 0.01 m in 5 minutes. Find out the temperature of the lower surface of the tank. Thermal conductivity of steel = 0.012 SI units and latent heat of steam = 540 kcal/kg.
Soln.: The flow of heat across the bottom width of the tank is
Q=K (A(θ_1-θ_2)t)/x kcal. Here, θ1 = temperature of the lower surface of the tank bottom =? ; θ2 = temperature of the upper surface of the tank bottom = normal boiling temperature of water = 100 0C ; A = surface area of the tank bottom in m2 ; x = thickness of the tank bottom = 2 × 10-3 m ; t = 5 × 60 sec = 300 sec.
Moreover, fall of water level in 5 minutes = dx = 0.01 m and density of water = ρ = 103 kg/m3. Now mass of water evaporated in 5 minutes = volume × density = (A × dx) × ρ = A × 0.01 × 103 = A × 10 kg.
Heat required to evaporate this amount of water = mass × latent heat of steam = A × 10 × 540 = A × 5400 kcal. This should be the heat conducted from the lower surface to the upper surface of the tank bottom in 5 minutes.
Hence
A ×5400=K (A(θ_1-θ_2)t)/x=0.012×A(θ_1-100)×300/2 × 10-3
∴θ1 = 1030C.